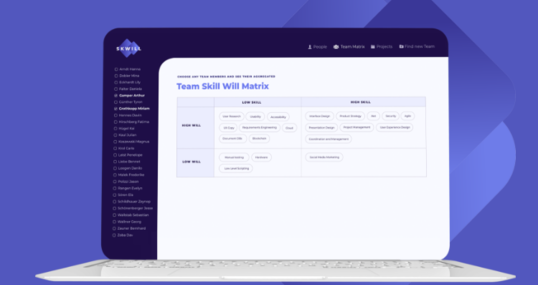
Introduction
When it comes to advanced driver-assistance systems or self-driving cars, one needs to find a way of estimating the distance to other vehicles on the road. One creative approach to achieve this goal would be to detect license plates in the real-time footage recorded by the cameras installed in a car. The standardized size of license plates enables us to compute the distance to the car in front by doing some computations using the detected bounding box. Besides, this information can help to better differentiate cars from other vehicles and objects on the road.
In this blog post, resulting from joint work with Aigiz Kunafin (TIMETOACT GROUP Austria Data Science), we try to build an algorithm as sketched above and fine-tune it to achieve decent performance.

Final license plate detection as well as derived and true distance
Detecting license plates
At the beginning of every data science project is the need for appropriate data. For our purposes we need images of cars with license plates of equal size and look. Together with these images we require information about the position of plates in the image as well as the real distance from the camera to the car.
Once we have collected this data, we need an algorithm capable of detecting objects in an image reliably and in real-time. For this purpose, the YOLOv5 architecture is one of the most popular choices as it is highly performant while being extremely small [1]. Based on the machine learning framework PyTorch, there are five different pre-trained models balancing the trade-off between high accuracy and fast detection times. As we want fast predictions and reasonable accuracy, we chose the medium sized model balancing both requirements.
Having found an appropriate pre-trained model for object detection, we want to fine tune it to detect license plates in the next step. By applying data augmentation, i.e. altering the training images for every training batch, we can extend our existing data and enable our model to generalize better (check sample images below). Note that the existing images are not only randomly flipped and tilted but also cut and combined with other images. As the training images are different in every training step, the model is forced to actually learn the concept of a license plate in different scenarios. This reduces the risk of overfitting to the training images.

Training batch samples demonstrating data augmentation
Doing the math
Computing the distance
Once we have a reliable and accurate model at hand its predictions provide us with information about the width of the found license plate in pixels (W_pixel). Knowing the real width (W_real) of a license plate, which is 52 cm, and applying triangle similarity we can derive the distance of the car to the camera (D):
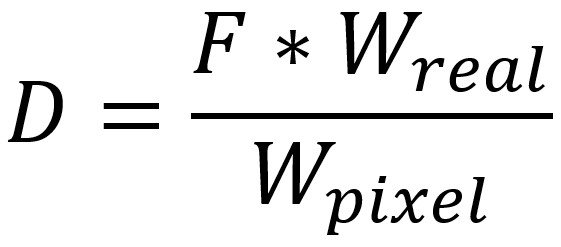
The only part missing is focal length (F). This factor can, however, be extracted from the technical metadata saved in the jpg files. As we have to correct some variables of the data a few more computational adaptations are necessary (check out details here [2]).
Angle correction refinement
So far, our model is only capable of detecting bounding boxes parallel to the image boundaries. This can be problematic as license plates are not necessarily horizontally aligned. Besides the width of a license plate also its height is standardized. We can hence utilize the information about this constant ratio and correct for the fact that a bounding box of a tilted license plate will have a larger height. In the image below, for example, the license plate width used for our calculations (W_real) gets corrected. Instead of the real width of 52 cm the calculations yield that we should use a width of 51,88 cm. This compensates the tilt, which would otherwise cause our predicted bounding box width to be too small and thus lead to an overestimation of the distance.

Putting it all together
Finally, we can combine detection and computations to estimate the distance.
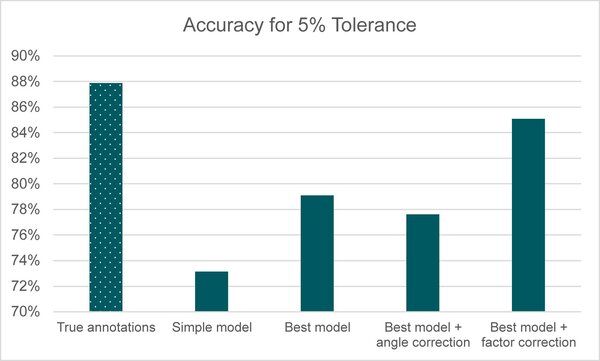
The graphs below show the quality of different versions of the model by comparing the predicted distance with the true distance of the test data. The mean relative error (MRE) provides insight into the average deviation from the true distance while the mean squared error (MSE) particularly penalizes large mistakes. This means, we aim at achieving low values in both cases. Besides, we can compare the approaches based on how many of the test images have a deviation of at most 5% of the true distance. This metric should thus be as high as possible.
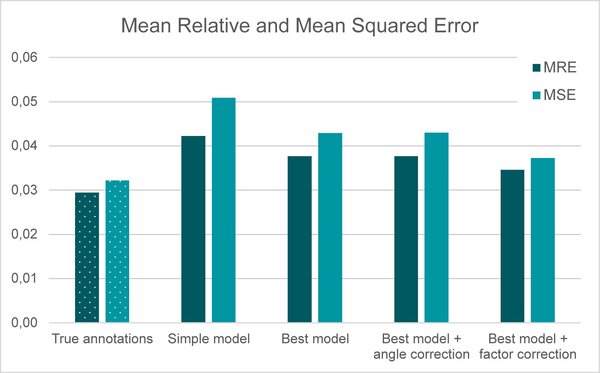
True annotations: For this model, we do not use object detection for detecting license plates, but rather combine the true license plate width in the image with the distance computation. By using these “true” positions we try to set a baseline of what could be achieved in the best case by our computations. The reason for this being not at 100% lies in several possible biases, like imprecise focal lengths, true annotations and distance measures in our data. Unfortunately, testing has shown that the angle refinement led to almost no improvement in this setting
Simple model: This model uses an object detection model where the training data has not been augmented. Compared to the baseline, the simple model already performs quite well but there is room for improvement.
Best model: An extension of the simple model where the object detection model has been trained with augmented data. For this model, the metrics improve noticeably. As the pre-assessment already suggested, the angle correction does not lead to the expected improvement. However, inspection of our predictions showed that we systematically underestimate the distance. This might be caused by a slight bias in our focal length computation. Correcting for this factor leads to another major improvement. Applying the final model, we can predict the distance to a car in front in 85% of the cases right with 5% tolerance.
Additionally, the best model trained detects license plates in almost all test images (except for one). While the simple model was unable to detect anything in six out of 72 test images (cf. technical appendix). This can be attributed to higher generalization power due to data augmentation, which is particularly important for real-world deployment.
Conclusion
In summary, we were able to build a powerful algorithm to estimate the distance to a car in front based on images and by utilizing the standard dimensions of a license plate. Using the fast YOLOv5 model, we would be able to operate in real-time with great accuracy. Testing on the validation set for a range of around 1 to 8.5 meters showed that we can estimate the distance correctly within a small tolerance in 85% of the cases. Moreover, we are on average only 3,5% off the true distance.
This algorithm could thus be an effective and efficient solution instead of ultrasonic sensors, as cameras and powerful computers are usually already built into cars for other advanced driver-assistance systems. Making use of additional cameras installed in a car, accuracy of the distance estimation could be increased further as this would allow to combine positional information from different angles. Additionally, utilizing the detected license plates can help to differentiate between cars and other objects on the road with higher certainty. After all, looking at the current capabilities of this algorithm from a broader perspective, numerous further applications can emerge.
[1] Cf. GitHub - ultralytics/yolov5: YOLOv5 🚀 in PyTorch > ONNX > CoreML > TFLite , YOLOv5 is Here!
[2] OpenCV: How-to calculate distance between camera and object using image?
Technical appendix
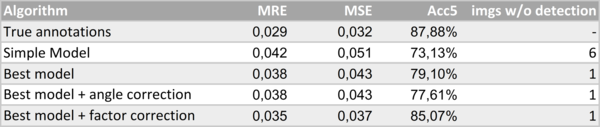
Collected numerical results (to achieve full comparability, best model and the true annotation approach were evaluated on the images where also the simple model detected license plates).
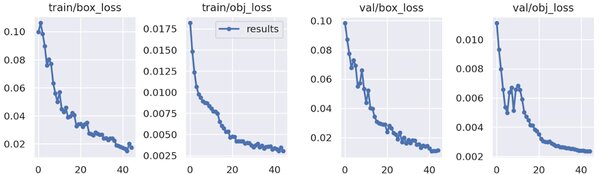
Training process of the final model. The two left images show the decrease in box and object loss for the train set, the images to the right for the test set after each training epoche.